Wi-Fi: Throughput variation with distance
Introduction#
In this experiment we will study how the downlink UDP throughput from an Access Point (AP) and a Station (STA) varies with the distance between these two devices. While the wireless link scheduling mechanism remains the same (as per the standard), the bit rate at which the AP and STA digital transceivers reliably operate depends on the received signal power at the receiver (i.e., the PHY rate), and the noise plus interference at the receiver. In this experiment, since we have only one AP-STA pair, there is no interference. Further, since the STA has no data to send, there is also no contention. Hence, the transfer of UDP packets from the AP to the STA comprises alternating back-off periods at the AP and packet transmission times. The back-off periods are random but from the initial back-off distribution. The transmission times depend on the PHY rate. Thus, effective transmission time will vary as per the following express
$$MeanEffectiveTransmissionTime = MeanInitialBackoff + PacketOverhead + \frac{PacketLength}{PHYRate}$$
Of the three terms on the right, the third term depends on the AP-STA distance, since the PHY rate decreases for increasing distance. Since we are interested in the packet throughput, we can write:
$$PacketThroughput = 1/MeanEffectiveTransmissionTime$$
The above expression is correct only if every packet sent by the AP is correctly decoded by the STA. Even if the PHY rate is correctly chosen so that the SNR at the mean received power renders every packet decodable, in practice, the received power varies randomly due to the phenomenon of shadowing and multipath fading. Due to these phenomena, while the mean received power may be adequate, the actual received power can drop so much that there are packet losses. Although, NetSim can model the phenomenon of shadowing and fading for this experiment we turn this feature off and consider a constant pathloss model.
Simplified pathloss model#
The complexity of signal propagation makes it difficult to obtain a single model that characterizes path loss accurately across a range of different environments. For general tradeoff analysis of various system designs it is sometimes best to use a simple model that captures the essence of signal propagation without resorting to complicated path loss models, which are only approximations to the real channel anyway. The following simplified model for path loss as a function of distance is commonly used for system design:
$$P_{r} = P_{t} \times c_{0} \times \left( \frac{d_{0}}{d} \right)^{\eta}$$
In this approximation, $P_{r}$ is the received power sometimes called received signal strength (RSS), $P_{t}$ is the transmit power, $c_{0}$ is the path loss at the "reference" distance, $d_{0}$ (usually 1m), $\eta$ is the path-loss exponent and $d$ is the distance between the transmitter and the receiver. The dB attenuation is thus
$$P_{r}(dBm) = P_{t}(dBm) + c_{0}\ (dB) - 10 \times \eta \times \log_{10}\left( \frac{d}{d_{0}} \right)$$
As $d\ $increases, the received power decreases, e.g., doubling the distance reduces the received power by approximately $3\eta$, since $\log_{10}{2 \approx 0.3}$. Typical values of $\eta$, indoors, could be 3 to 5, resulting in 9 dB to 15 dB additional path loss for doubling the value of $d$.
The IEEE 802.11g PHY Rates Table#
IEEE 802.11g utilizes OFDM over the entire 20 MHz channel. There are 52 OFDM carriers, of which 48 carriers are used for data transmission and 4 are used for control. The OFDM symbol rate is 250 Ksps. With 48 symbols being sent together (across the 48 carriers), we obtain 12 Msps. In principle, each symbol can be modulated according to any of the modulation and coding schemes (MCS) shown in Table 1. The bit rate shown in the last column of the table assumes the situation in which all the symbols are modulated using the same MCS. Thus, for example, the MCS in the row indexed by 4 uses 16 QAM (i.e., 4 bits per symbol) with a coding rate of 1/2 (i.e., half the bits are data bits, and the rest are channel error protection bits), yielding 2 data bits per symbol, and, therefore, 24 Mbps overall bit rate, assuming that all OFDM symbols use the MCS.
MCS stands for modulation and coding scheme. The MCS defines the numbers of useful bits which can carried by one symbol. In WiFi IEEE 802.11g standard, the MCS depends on the received signal strength (RSS). The higher the signal strength the higher the MCS and more useful bits can be transmitted in a symbol. Thus, the PHY bit rate depends on the MCS chosen. IEEE 802.11g devices can transmit at speeds of 6, 9, 12, 18, 24, 36, 48 and 54Mbps as shown in the table below.
Index Rx Sensitivity (dBm) Modulation Code Rate Bit Rate
0 -82 BPSK $$1/2$$ 6 Mbps
1 -81 BPSK $$3/4$$ 9 Mbps
2 -79 QPSK $$1/2$$ 12 Mbps
3 -77 QPSK $$3/4$$ 18 Mbps
4 -74 16 QAM $$1/2$$ 24 Mbps
5 -70 16 QAM $$3/4$$ 36 Mbps
6 -66 64 QAM $$2/3$$ 48 Mbps
7 -65 64 QAM $$3/4$$ 54 Mbps
: Table 1: 802.11g bit rates for different modulation schemes, and the minimum received signal power for achieving each bit rate.
In the above table, Rx Sensitivity is the minimum RSS. A simulation assumption in NetSim is that the transmitter knows the RSS at the receiver. Thus, the transmitter chooses the MCS by comparing the RSS against the Receiver-Sensitivity for different MCSs. The highest possible MCS is then chosen.
Calculating distances at which the PHY rate changes#
In this section, we predict the AP-STA distance thresholds for the different PHY rates. We know that
$$P_{r} = P_{t} - c_{0} - 10\ \eta\ log_{10}\ (d)$$
At 2.4 GHz, $c_{0}$ is $40.09\ dB$. For $P_{t} = 100\ mW\ (20\ dBm)$, $\eta = 3.5,$ and setting $P_{r}$ as equal to the receive sensitivity (Ref: Table 1), and we get the following inequality for the 6 Mbps PHY rate
$$- 82 \leq 20 - 40.09 - 35 \times \log{(d) < \ - 81}$$
This gives $54.99m < \ d \leq 58.72\ m.$ Similarly, we compute the AP-PHY distance for all the rates and arrive at the table below
Rx Sensitivity (dBm) Bit Rate $$\mathbf{d}{\mathbf{\max}}\mathbf{\ (m)}$$ $\mathbf{d}}\mathbf{\ (m}$)
-82 6 Mbps 58.72 55.00
-81 9 Mbps 54.99 48.22
-79 12 Mbps 48.21 42.28
-77 18 Mbps 42.27 34.69
-74 24 Mbps 34.68 26.68
-70 36 Mbps 26.67 20.52
-66 48 Mbps 20.50 19.20
-65 54 Mbps 19.19 1.00
: Table 2: We see the maximum and minimum AP-STA distances for different 801.11g PHY bit rates. The PHY rate is 0 for $d \geq 58.72m$. We have chosen $P_{t} = 100\ mW\ $and $\eta = 3.5.$
Rx Sensitivity (dBm) Bit Rate $$\mathbf{d}{\mathbf{\max}}\mathbf{\ (m)}$$ $\mathbf{d}}\mathbf{\ (m}$)
-82 6 Mbps 58.72 55.00
-81 9 Mbps 54.99 48.22
-79 12 Mbps 48.21 42.28
-77 18 Mbps 42.27 34.69
-74 24 Mbps 34.68 26.68
-70 36 Mbps 26.67 20.52
-66 48 Mbps 20.50 19.20
-65 54 Mbps 19.19 1.00
: Table 3: Predicted application throughput for various PHY rates
Table 2 can be visualized as shown below.
 {width="6.268055555555556in"
height="3.4159722222222224in"}
{width="6.268055555555556in"
height="3.4159722222222224in"}
Figure 10‑1: Illustration of variation in AP data (PHY) rate vs. distance for $P_{t} = 100\ mW$ and $\eta = 3.5$
Predicting the throughput#
From the experiment Wi-Fi-UDP-Download-Throughput we know that application throughput, $\theta$ is
$$\theta = \ \frac{Application\ Payload\ in\ Packet\ (bits)}{Average\ Time\ per\ Packet(µs)}$$
$$Average\ time\ per\ packet\ \ (µs) = \ DIFS\ + \ Average\ Backoff\ time\ + \ Packet\ Transmission\ Time\ + \ SIFS\ + \ ACK\ Transmission\ Time$$
Therefore,
$$\theta = \frac{L_{pkt} \times 8}{T_{DIFS} + \left( \frac{CW_{\min}}{2} \times T_{slot} \right) + \left( T_{preamble} + \frac{{(L}{pkt} + OH) \times 8}{PHYRate}\ \right) + T + \left( T_{preamble} + \frac{L_{ACK} \times 8}{PHYRate_{\min}} \right)}\ $$
In the above formula $\theta$ is in Mbps as the time in the denominator is in $\mu s$.
The predicted application throughput for a 1460B packet, with 68B overheads, ACK size of 14B, and PHY Rate of 54 Mbps is
$$\theta = \frac{1450 \times 8}{34 + \left( \frac{15}{2} \times 9 \right) + \left( 20 + \frac{(1450 + 68) \times 8}{54} \right) + 16 + \left( 20 + \frac{14 \times 8}{6} \right)} = \frac{11600}{401.04} = 28.92\ Mbps\ $$
Doing the same computation for the different PHY rates leads to the following application throughput predictions. Users just need to replace 54 in the above equation with the appropriate PHY rate.
PHY rate (Mbps) Predicted Application Throughput (Mbps)
54 28.92
48 27.02
36 22.59
24 17.00
18 13.63
12 9.76
9 7.60
6 5.27
In the following section we create scenarios with varying AP-STA distances in NetSim, model the same pathloss equation and compare simulation results against predictions.
Network Setup#
Open NetSim and click on Experiments> Internetworks> Wi-Fi> Impact of distance on Wi-Fi throughput then click on the tile in the middle panel to load the example as shown in below Figure 10‑2.
 {width="6.268055555555556in"
height="3.3520833333333333in"}
{width="6.268055555555556in"
height="3.3520833333333333in"}
Figure 10‑2: List of scenarios for the example of Impact of distance on Wi Fi throughput
NetSim UI displays the configuration file corresponding to this experiment as shown below in Figure 10‑3.
 {width="4.200400262467191in"
height="2.773659230096238in"}
{width="4.200400262467191in"
height="2.773659230096238in"}
Figure 10‑3: Network set up for studying the Impact of distance on Wi-Fi throughput
Procedure#
The following set of procedures were done to generate this sample.
Step 1: A network scenario is created in NetSim GUI comprising of 1 Wired Node, 1 Router, 1 Access Point and 1 Wireless Node in the "Internetworks" Network Library.
Step 2: In Access Point and Wireless Node 4, the Interface 1 (WIRELESS) > Physical Layer, Protocol Standard is set to IEEE802.11g and in the Interface 1 (WIRELESS) > Datalink Layer, Rate Adaptation is set to False.
Step 3: The position of the Wireless Node and the Access Point in the grid environment is set according to the values given in the below table see Table 10‑4.
Device
Positions
**Wireless Node 4** **Access Point**
X 250 250
Y 10 0
Table 10‑4: Device Positions
Step 4: Right click on Wireless Node and Access Point, select Properties, and select DCF as the Medium Access Protocol in the DATALINK_LAYER of INTERFACE_1
Step 5: Right-click the link ID (of a wired/wireless link) and select Properties to access the link's properties. The parameters are set according to the values given in the below table Table 10‑5/Table 10‑6.
Wired Link Properties
Max Uplink Speed (Mbps) 100
Max Downlink Speed (Mbps) 100
Uplink BER 0
Downlink BER 0
Uplink Propagation Delay (µs) 0
Downlink Propagation Delay (µs) 0
Table 10‑5: Wired link Properties
Wireless Link Properties
Channel Characteristics Path Loss Only
Path Loss Model Log Distance
Path Loss Exponent 3.5
Table 10‑6: Wireless Link Properties
Step 6: Right click on App1 CBR and select Properties or click on the Application icon present in the top ribbon/toolbar.
A CBR Application is generated from Wired Node 2 i.e., Source to Wireless Node 4 i.e., Destination with Packet Size set to 1450 Bytes and Inter Arrival Time set to 200 µs. It is set such that, the Generation Rate equals to 58 Mbps.
Transport Protocol is set to UDP instead of TCP.
Step 7: Packet Trace is enabled in NetSim GUI. At the end of the simulation, a very large .csv file is containing all the packet information is available for the users to perform packet level analysis.
Step 8: Plots are enabled in NetSim GUI. Run simulation for 10 sec.
Go back to the scenario and change the distance between Access Point and Wireless Node (i.e., Change the Y axis of Wireless Node (STA)) as 20, 25, 30, 35, 45, 50, 55 and 60.
Simulation Output#
Data rate can be calculated from packet trace by using the formula given below:
$$PHYRate\ (Mbps) = \frac{PHYLayerPayload\ (B) \times 8}{PHYEndTime\ (\mu s) - PHYArrivalTime(\mu s) - 20(\mu s)}$$
$20\mu s\ $is the preamble time for 802.11g.
Given below are the steps to calculate the PHY rate for a 10m AP-STA distance of STA using the packet trace.
Step 1: Make sure that the packet trace is enabled before the simulation, and then run the simulation for a desired time.
Step 2: Click on 'Open Packet Trace'.
Step 3: Filter CONTROL_PACKET_TYPE/APP_NAME as App1_CBR (Only data packets) and TRANSMITTER_ID as ACCESSPOINT-1 (Only wireless channel).
Step 4: Add a column 'Phy Rate (Mbps)' after PHY_LAYER_PAYLOAD(Bytes)
Step 5: Add formula in the first cell of newly added column.
=([@[PHY_LAYER_PAYLOAD(Bytes)]]*8)/([@[PHY_LAYER_END_TIME(US)]]-[@[PHY_LAYER_ARRIVAL_TIME(US)]]-20)
Step 6: We get the Phy Rate as 54Mbps. (The column Phy Rate is formatted to zero decimal places)
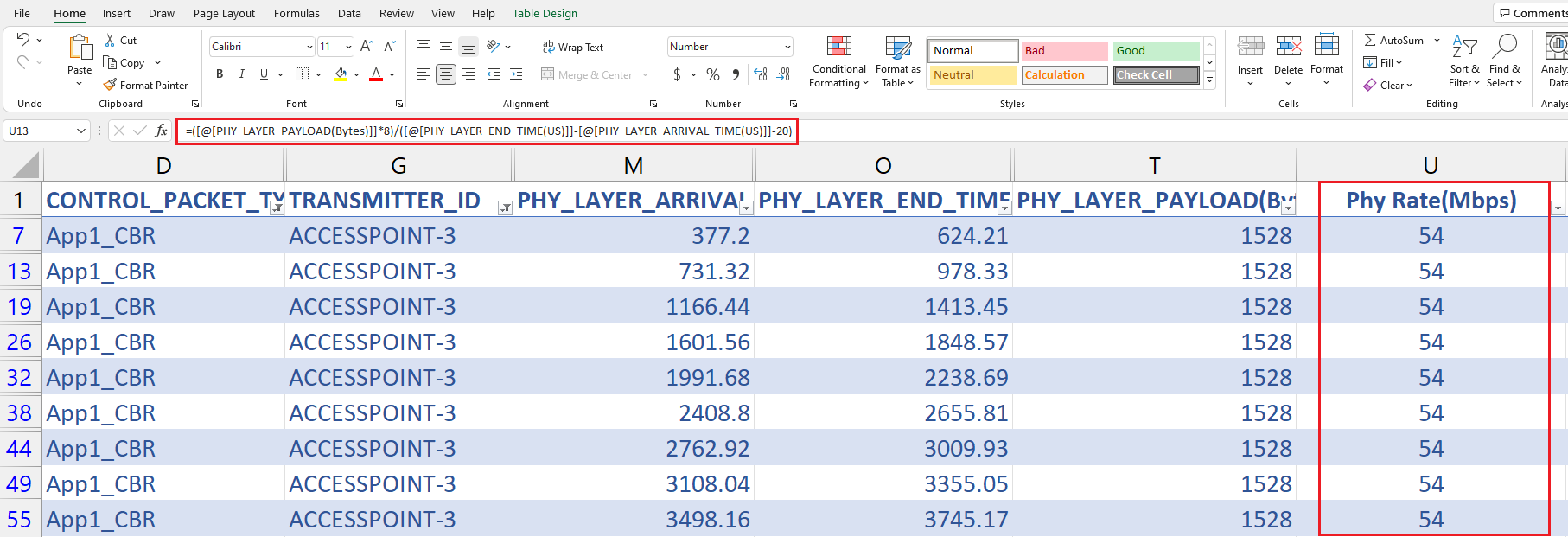 {width="6.268055555555556in"
height="2.1458333333333335in"}
{width="6.268055555555556in"
height="2.1458333333333335in"}
Figure 10‑4: Calculating the Phy Rate using its formula in packet trace.
Results#
Simulation results with PHY rates and application throughputs are tabulated in Table 10‑7.
+-----------+--------+-----------+---------+-----------+-------------+ | 802.11g | | | | | | | PHY rate | | | | | | | and | | | | | | | Ap | | | | | | | plication | | | | | | | T | | | | | | | hroughput | | | | | | | Com | | | | | | | parison | | | | | | +===========+========+===========+=========+===========+=============+ | $ | | PHY | PHY | Ap | | | \mathbf{d | Sample | rate | Rate | plication | Application | | }_{\mathb | Di | NetSim | | T | Throughput | | f{\min}}\ | stance | (Mbps) | Pr | hroughput | Predicted | | mathbf{-} | (m) | | edicted | NetSim | (Mbps) | | \mathbf{d | | | ( | (Mbps) | | | }_{\mathb | | | Mbps) | | | | f{\max}}$ | | | | | | | (m) | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 0 - 19.19 | 10 | 54 | 54 | 29.15 | 28.92 | +-----------+--------+-----------+---------+-----------+-------------+ | 19.20 - | 20 | 48 | 48 | 27.24 | 27.02 | | 20.50 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 20.51 -- | 25 | 36 | 36 | 22.71 | 22.59 | | 26.67 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 26.68 -- | 30 | 24 | 24 | 17.09 | 17.00 | | 34.68 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 34.69 -- | 40 | 18 | 18 | 13.68 | 13.63 | | 42.27 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 42.28 -- | 45 | 12 | 12 | 9.79 | 9.76 | | 48.21 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 48.22 -- | 50 | 9 | 9 | 7.61 | 7.60 | | 54.99 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | 55.00 -- | 57 | 6 | 6 | 5.28 | 5.27 | | 58.71 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+ | Beyond | 60 | 0 | 0 | 0 | 0 | | 58.72 | | | | | | +-----------+--------+-----------+---------+-----------+-------------+
Table 10‑7: We see how PHY rate, Application Throughput varies with AP-STA distance
Figure 10‑5: Data Rate vs. Distance
Figure 10‑6: Application Throughput vs. Distance
10.10 Discussion#
It is interesting to note that for 54Mbps PHY rate the application throughput is 29.21 Mbps, which is about 54.1% of the PHY rate. However, for 6 Mbps PHY rate the application throughput is 5.28 Mbps which is 88% of the PHY rate. Why is this so?
Let us go back to the average time per packet -- the denominator of the throughput expression - which is
$$T_{DIFS} + \left( \frac{CW_{\min}}{2} \times T_{slot} \right) + \left( T_{preamble} + \frac{{(L}{pkt} + OH) \times 8}{PHYRate}\ \right) + T + \left( T_{preamble} + \frac{L_{ACK} \times 8}{PHYRate_{\min}} \right)$$
Per the 802.11g standards the 14 Byte MAC ACK is always sent at the control rate or $PHYRate_{\min}$ which is 6 Mbps. Therefore, all terms in the above expression except $\frac{{(L}_{pkt} + OH) \times 8}{PHYRate}$ do not vary with the PHY rate.
We observe that, since all the "overheads" do not decrease with PHY rate, the lower PHY rates are more "efficient" than the higher PHY rates. This motivates the aggregation of packets in the newer standards (11n, 11ac, etc.), so that the fixed overheads are amortized over large number of data bits.
10.11 Conclusion#
To summarize, we understood the log distance pathloss model and saw how WiFi PHY rates and Application throughputs vary with AP-STA distance. Then we predicted the WiFi PHY rate and application throughputs. Simulation results show excellent agreement with theory.
References#
Some of the theoretical content is from the books (i) Wireless Communications by Andrea Goldsmith, and (ii) Wireless Networking by Anurag Kumar.
Exercises#
-
Keeping other variables fixed, change the transmit power ${(P}_{t})$ to a different value. Predict $d$ for different PHY rates. Compare against simulation
-
Keeping other variables fixed, change the pathloss exponent $\eta$ (generally in the range of 2 to 5). Predict $d$ for different PHY rates. Compare against simulation.
-
Keeping other variables fixed, change the packet size $L_{pkt}$ (from between 100B to 1460B). Take care to ensure the generation rate is sufficiently high to ensure full buffers (saturation) at the transmitting node. Predict $\theta$ for different PHY rates. Compare against simulation
