Understand the working of TCP BIC Congestion control algorithm, simulate and plot the TCP congestion window
Theory#
In BIC congestion control is viewed as a searching problem in which the system can give yes/no feedback through packet loss as to whether the current sending rate (or window) is larger than the network capacity. The current minimum window can be estimated as the window size at which the flow does not see any packet loss. If the maximum window size is known, we can apply a binary search technique to set the target window size to the midpoint of the maximum and minimum. As increasing to the target, if it gives any packet loss, the current window can be treated as a new maximum and the reduced window size after the packet loss can be the new minimum. The midpoint between these new values becomes a new target. Since the network incurs loss around the new maximum but did not do so around the new minimum, the target window size must be in the middle of the two values. After reaching the target and if it gives no packet loss, then the current window size becomes a new minimum, and a new target is calculated. This process is repeated with the updated minimum and maximum until the difference between the maximum and the minimum falls below a preset threshold, called the minimum increment (S~min~). This technique is called binary search increase.
Additive Increase#
In order to ensure faster convergence and RTT-fairness, binary search increase is combined with an additive increase strategy. When the distance to the midpoint from the current minimum is too large, increasing the window size directly to that midpoint might add too much stress to the network. When the distance from the current window size to the target in binary search increase is larger than a prescribed maximum step, called the maximum increment (Smax) instead of increasing window directly to that midpoint in the next RTT, we increase it by Smax until the distance becomes less than Smax, at which time window increases directly to the target. Thus, after a large window reduction, the strategy initially increases the window linearly, and then increases logarithmically. This combination of binary search increase and additive increase is called as binary increase. Combined with a multiplicative decrease strategy, binary increase becomes close to pure additive increase under large windows. This is because a larger window results in a larger reduction by multiplicative decrease and therefore, a longer additive increase period. When the window size is small, it becomes close to pure binary search increase -- a shorter additive increase period.
Slow Start#
After the window grows past the current maximum, the maximum is unknown. At this time, binary search sets its maximum to be a default maximum (a large constant) and the current window size to be the minimum. So, the target midpoint can be very far. According to binary increase, if the target midpoint is very large, it increases linearly by the maximum increment. Instead, run a "slow start" strategy to probe for a new maximum up to Smax. So if cwnd is the current window and the maximum increment is Smax, then it increases in each RTT round in steps cwnd+1, cwnd+2, cwnd+4,,, cwnd+Smax. The rationale is that since it is likely to be at the saturation point and also the maximum is unknown, it probes for available bandwidth in a "slow start" until it is safe to increase the window by Smax. After slow start, it switches to binary increase.
Fast Convergence#
It can be shown that under a completely synchronized loss model, binary search increase combined with multiplicative decrease converges to a fair share. Suppose there are two flows with different window sizes, but with the same RTT. Since the larger window reduces more in multiplicative decrease (with a fixed factor β), the time to reach the target is longer for a larger window. However, its convergence time can be very long. In binary search increase, it takes $\log(d) - \log(Smin)$ RTT rounds to reach the maximum window after a window reduction of d. Since the window increases in a log step, the larger window and smaller window can reach back to their respective maxima very fast almost at the same time (although the smaller window flow gets to its maximum slightly faster). Thus, the smaller window flow ends up taking away only a small amount of bandwidth from the larger flow before the next window reduction. To remedy this behaviour, binary search increase is modified as follows. After a window reduction, new maximum and minimum are set. Suppose these values are max_wini and min_wini for flow i (i =1, 2). If the new maximum is less than the previous, this window is in a downward trend. Then, readjust the new maximum to be the same as the new target window (i.e. max_wini = (max_wini-min_wini)/2), and then readjust the target. After that apply the normal binary increase. This strategy is called fast convergence.
Network setup#
Open NetSim and click on Experiments> Internetworks> TCP> Advanced TCP BIC Congestion control algorithm then click on the tile in the middle panel to load the example as shown below in Figure 33‑1.
 {width="6.445108267716535in"
height="3.4583333333333335in"}
{width="6.445108267716535in"
height="3.4583333333333335in"}
Figure 33‑1: List of scenarios for the example of Advanced TCP BIC Congestion control algorithm
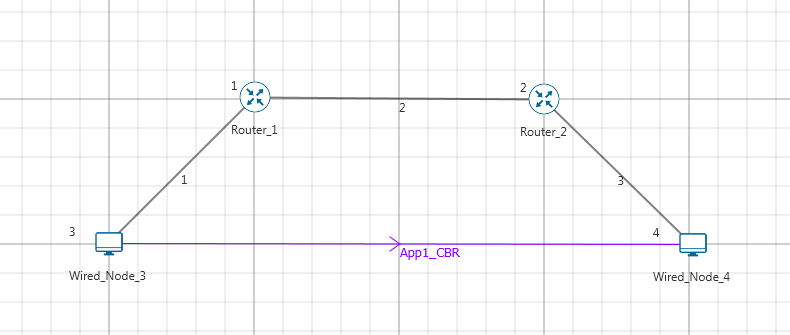
NetSim UI displays the configuration file corresponding to this experiment as shown below Figure 33‑2.
 {width="4.680748031496063in"
height="1.9849475065616797in"}
{width="4.680748031496063in"
height="1.9849475065616797in"}
Figure 33‑2: Network set up for studying the Advanced TCP BIC Congestion control algorithm
Procedure#
The following set of procedures were done to generate this sample:
Step 1: A network scenario is designed in NetSim GUI comprising of 2 Wired Nodes and 2 Routers in the "Internetworks" Network Library.
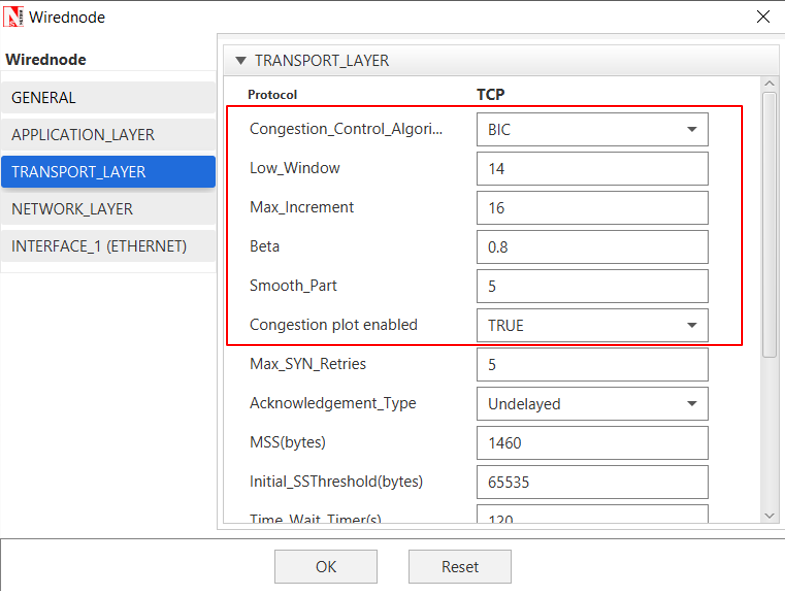
Step 2: In the General Properties of Wired Node 3 i.e. Source, Wireshark Capture is set to Online and in the TRANSPORT LAYER Properties, Window Scaling is set as TRUE.
Step 3: For all the devices, in the TRANSPORT LAYER Properties, Congestion Control Algorithm is set to BIC. But the congestion plot is set to TRUE only in Wired_Node_3.
 {width="4.213117891513561in"
height="3.1496062992125986in"}
{width="4.213117891513561in"
height="3.1496062992125986in"}
Figure 33‑3: Transport Layer window
Step 4: The Link Properties are set according to the table given below Table 33‑1.
Link Properties Wired Link 1 Wired Link 2 Wired Link 3
Uplink Speed (Mbps) 100 20 100
Downlink Speed (Mbps) 100 20 100
Uplink propagation delay (µs) 5 1000 5
Downlink propagation delay 5 1000 5 (µs)
Uplink BER 0.00000001 0.00000001 0.00000001
Downlink BER 0.00000001 0.00000001 0.00000001
Table 33‑1: Wired Link Properties
Step 5: Right click on the Application Flow App1 CBR and select Properties or click on the Application icon present in the top ribbon/toolbar.
A CBR Application is generated from Wired Node 3 i.e. Source to Wired Node 4 i.e. Destination with Packet Size set to 1460 Bytes and Inter Arrival Time set to 400 µs. Additionally, the "Start Time" parameter is set to 20 Seconds.
The Packet Size and Inter Arrival Time parameters are set such that the Generation Rate equals 140 Kbps. Generation Rate can be calculated using the formula:
$$Generation\ Rate\ (Mbps)\ = \ Packet\ Size\ (Bytes)\ *\ 8/Interarrival\ time\ (µs)$$
Step 6: Plots are enabled in NetSim GUI. Click on Run simulation. The simulation time is set to 100 seconds.
Output#
 {width="6.5in"
height="4.216666666666667in"}
{width="6.5in"
height="4.216666666666667in"}
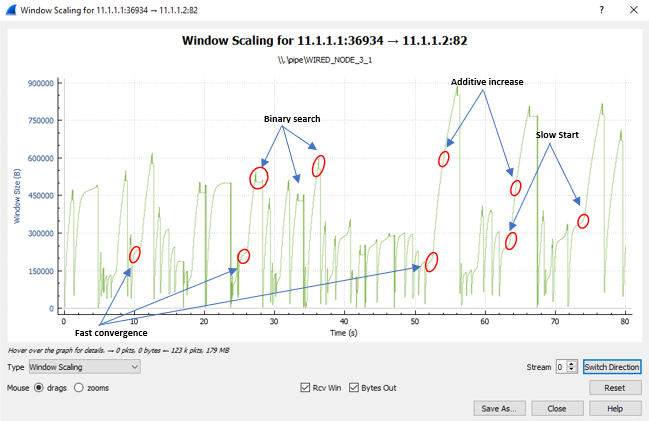
Figure 33‑4: Plot of Window Scaling in Wireshark Capture
Note: User need to "zoom in" to get the above plot.
Go to the Wireshark Capture window.
Click on data packet i.e.\<None>. Go to Statistics TCP Stream Graphs Window Scaling.
Click on Switch Direction in the window scaling graph window to view the graph.
(For more guidance, refer to section - 8.7.5 Window Scaling" in user manual)
The graph shown above is a plot of Congestion Window vs Time of BIC for the scenario shown above. Each point on the graph represents the congestion window at the time when the packet is sent. You can observe Binary Search, Additive Increase, Fast Convergence, Slow Start phases in the above graph.
